Closure of Relations and Languages
Closure of Relations
Let S be a set and
R ⊆ S x S be a relation on S. The following correspondences exist:
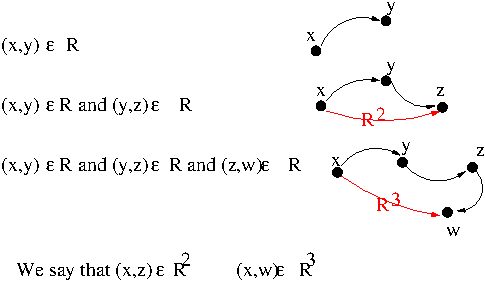
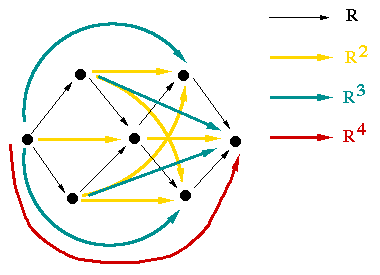
That is, we can form new relations Ri where i is a path of length i,
because, by applying R twice we can relate x and z; by applying R three
times we can relate x and w, etc.
Also, even though I haven't drawn it in, (y,w) ∈ R2 because R2 is all paths of
length 2.
In general, (x0,xn) ∈ Rn iff there exists x0,x1,x2,...xn-1,xn
∈
S such that (x0,x1),(x1,x2),...,(xn-1,xn)
∈ R iff there exists a path in G: 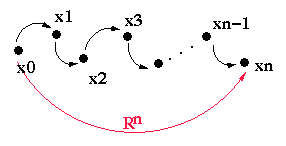
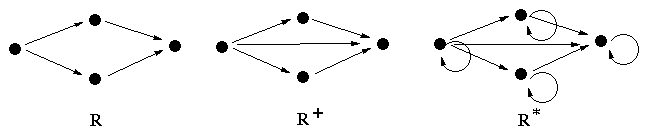
Now, 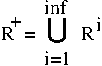 is called the transitive closure of R.
is called the transitive closure of R.
Thus:
- R ⊂ R+
- (x,y) ∈ R+ and (y,z) ∈ R -> (x,z) ∈ R+.
- Nothing is in R+ except by virtue of 1. and 2.
The reflexive transitive closure of R is
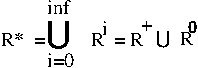 This differs from the transitive closure in that we add
This differs from the transitive closure in that we add
R0 = {(a,a) | a ∈ S}
More Examples:
Closure of Languages (Sets)
Let L1 and L2 be languages (i.e., sets of strings). Then we define the
concatenation, or product of L1 and L2, denoted L1L2:
L1L2 = {xy | x ∈ L1 and y ∈ L2}
Specifically, let ∑ be an alphabet (so ∑ is a language.)
Then ∑ ∑ = ∑2 = {a1a2 | a1, a2 ∈ ∑ }
and, in general,
∑n =
{wa | w ∈ ∑n-1 and a ∈ ∑}
Now we define the following closures of ∑ under concatenation:

Remark: any string over ∑ of length >=0 is in ∑*, therefore
a language over ∑ is a subset of ∑*.



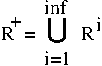 is called the transitive closure of R.
is called the transitive closure of R.
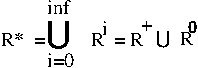 This differs from the transitive closure in that we add
This differs from the transitive closure in that we add


